実技競技詳細解説

実技競技❶ 解説
Challenge-18
実技競技①は、1チーム3名が協力し、配点の異なる18問の数学・情報に関する問題を解き、制限時間100分内に、正解した問題で得られた合計得点を競う競技であった。また、事前資料には出題される問題の6割程度はプログラムにより計算を行わなければ解答が得られないという旨が書かれていた。

今回の競技内容は競技プログラミングといわれる、与えられた要求を満足するプログラムを正確に記述するプログラミングコンテストと同じようなものであり、これらはコンピュータサイエンスや数学の知識を必要とする問題が多く出題されることが特徴である。

競技プログラミングは国内外問わず開催されており、AtCoder、Topcoder、ACM国際大学対抗プログラミングコンテストなど有名なコンテストが沢山存在する。特に今回の形式に非常に近いものとしてProject Eulerといわれるコンテストがある。このコンテストでは、挑戦しがいのある数学/コンピュータプログラムの問題が出題されており、これを解くためには単なる数学的洞察以上のものが必要とされる。

また、数学の知識があれば簡潔で効率的に問題を解くことができるが、多くの場合はコンピュータとプログラムの技能が必要とされる。

【素数】の問題は、ある決まった範囲の素数を印刷すると「1」は何回印刷されるかというものであった。範囲が小さいものであれば、直接プログラムを書くよりも紙に書いて数え上げた方が早いが、範囲が大きい場合は、どのように素数を求めるかというのが肝になる。有名な方法として「エラトステネスの篩ふるい」がある。

【竹内関数】とは、プログラミング言語処理系のベンチマークなどに使われる、再帰的に定義された関数であり、1974年に竹内郁雄によって考えられたものである。再帰的に定義されの関数には、フィボナッチ数列やアッカーマン関数などがある。

【2進法】の問題は、2進法で表されている数を10進法で表し直す問題であった。頑張ってプログラムを書いて求めることも出来れば、パソコンを電卓代わりに使って解くことも出来る。また、手計算で求めることも出来るが、ちょっとした工夫をすることで手計算でも効率よく簡単に求めることも出来る。色々な手法で求めることが出来る面白い問題であった。

【和が決められた数列】の問題は、自然数の分割に関する問題であった。自然数nに対して、その順番の違いを除いて自然数の和として表す方法の個数を分割数といいp(n)で表し、互いに異なる自然数に分割する方法の個数を異分割数といいq(n)で表し、自然数nに対して、奇数の自然数に分割する方法の個数を奇分割数という。このとき、問1はq(50)を求める問題であり、問2はp(50)を求める問題であった。また、問3は異分割数と奇分割数は等しいという「オイラーの分割恒等式」よりq(50)と同じ値になる。

【約数】の問題は、約数関数

に関する問題であった。特に、σ₀(n)=d(n)、σ₁(n)=σ(n)と表記されることもある。d(n)やσ(n)は具体的な求め方が知られており、

に対して

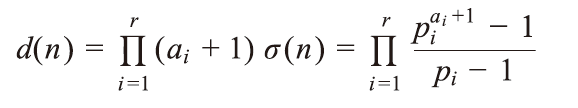
となる。余談であるが、σ(n)=2nとなるnは完全数として知られており、σ(n)=knとなるnはk倍完全数といわれている。つまり、完全数とは2倍完全数のことであると見ることも出来る。

【部分文字列】の問題は、部分集合の考え方に関する問題であった。文字が全て異なる長さnの文字列の部分文字列は、べき集合の考え方より2n個の部分文字列が出来る。文字が全て異なるとは限らない場合は、同様の方法で得られた2 n個の集合に対して和集合を考えれば、重複している部分が取り除けて題意の文字列の集合が得られる。今回の場合はn=11と小さいため、2048個の中から重複部分を取り除く方法でも現実的な時間で解くことが出来るが、nが大きい場合は、動的計画法による方法が現実的である。

重要な部分をザックリ説明すると、1文字目からk文字目までの文字を用いた部分文字列が出来ていたとする。これらの部分文字列とさらに末尾にk+1文字目を追加したものの和集合を求め、これを1文字目からk+1文字目までの文字を用いた部分文字列とする。以下これを繰り返して求めていく方法である。

【整数】の問題は、タクシー数、コラッツ予想、ゴールドバッハの予想などの整数論の未解決問題を、プログラミングを用いて味わう問題であった。以下に、これらの問題に関連することをいくつか述べることにする。

• タクシー数の問題の拡張として、次の命題が知られている。「すべての自然数Nに対し、3次曲線x³+y³=ｍがxもyも共に正となる少なくともN個の整点をもつ整数m0が存在する。」

• コラッツ予想の問題は、最初の方で見た「竹内関数」の問題に出題が似ており、共に再帰的な操作の回数を求める問題であった。また、2011年のセンター試験では、数学Ⅱ・Bの第6問の数値計算とコンピュータを出題テーマとした問題で、この問題と同様に有名なコラッツ予想をテーマとした問題が出題された。

• 普通ゴールドバッハの予想といわれると「全ての2よりも大きな偶数は、2つの素数の和として表すことができる」という内容を思い浮かべると思う。この予想の名前の由来は、1742年にゴールドバッハがオイラーへの書簡で「5より大きな任意の自然数は、3つの素数の和で表せる」と述べたことに由来する。また、類似の予想として「5より大きい奇数は、3つの素数の和で表せる」という「弱いゴールドバッハの予想」や「4より大きい偶数は、2つの奇素数の和で表せる」という「強いゴールドバッハの予想」などがある。

【ドレミ暗号】の問題は、複文字換字式暗号に関する問題であった。問1は実際にデコードするために必要な暗号文の構造を解析する問題であり、問2は実際に換字表を作成し、それに基づいてエンコードする問題であった。換字式暗号は小説などにも登場することがあり、有名なものではエドガー・アラン・ポーの黄金虫、江戸川乱歩の二銭銅貨、アーサー・コナン・ドイルのシャーロック・ホームズシリーズの踊る人形などがある。

【文字列操作】の問題は、関数による文字列操作の順序による問題であった。プログラミングをする上で、文字列や配列などの操作や分析の技術などは必要になってくるものであり、実際にどのように操作を行えば欲しい結果が得られるかということを考えさせる問題であった。

【数列操作】の問題は、配列操作や漸化式に関する問題であった。問1のようにnが小さい場合は、具体的に手計算で順に求めていくことが可能である。問2に関しては、実際にsnを書き出すことは大変であるが、tnに関しては漸化式を立てることが出来るので、そこまでいけば手計算でも求めることが出来る。

「競技の手引き」の競技趣旨にも書かれているように、社会では科学技術上の問題を解決するにあたり、コンピューターを使って複雑な計算を行うことが多い。また、身近な科学現象には、理科・数学・情報など色々なものが複雑に絡み合っており、プログラミングによって科学技術上の問題を解決していることも多い。今回の問題は、プログラミングによる問題解決の有用性や数学的思考の必要性を感じることが出来る非常に良い問題であった。
埼玉大学大学院理工学研究科　中川　幸一